Attention Mechanism
Older models like RNN, LSTM would focus on a sequence one word at a time, but the attention mechanism scans all the words in a given sentence simultaneously and determines which words are important to understand the context of the sentence.
If you read a sentence “The cat catches a rat because it was hungry” then you will naturally give more attention on the word “cat” than others to understand the meaning of the word “It”. This is what the attention mechanism follows. This will give you an overall idea of how the attention mechanism works.
Self Attention: How it Works
Self attention is the mechanism that enables each element in a sequence attends to all other elements including itself.
If you look at the given sentence
“The cat chased the mouse because it was hungry”
Here the word “It” refers to “cat”. The model needs to give more attention on the word “cat” than other words to correctly predict the relationship with “cat”.
Scaled Dot Product Attention
This is the standard attention mechanism used in Transformers. It calculates the dot product between query and key, scaled by square root of d_k, and applies softmax layer over the results to obtain attention weights.
Steps to Perform Attention Calculation
Step 1: Compute Queries, Keys, and Values
Self-attention allows the model to decide how much attention to pay to each other word from each word in a sentence, and for that the embedding of each token is projected into 3 vectors called Query, Key, and Value.
To create those vectors, we apply a method called linear transformation (multiplying embedding by learned weight metrics).
Here X represents the vector embedding obtained for each word above.
Math behind linear transformation
Let’s take the word “cat” for example. Assume 2 dimensional embedding [1, 0.5] is assigned instead of a large dimensional embedding (E.g., 512 or 768). The large dimensional vector embedding multiplied by the weight matrix cannot be fully shown here.
So we take 2 dimensional embedding as an example and show the calculations.
Compute the Query (Q) vector
Compute the Key (K) vector
Compute the Value (V) vector
Finally the vectors of the word “cat” are calculated as follows.
Query (Q): [1.15, 0.55]
Key (K): [0.8, 0.55]
Value (V): [0.6, 0.7]
The weight metrics for query, key, and value are learned values. Each of the learned weight metrics in Bert is 768 x 768 in size.
import torch
import torch.nn as nn
# Define Linear Layers for Query, Key, and Value projections
d_model = token_embeddings.size(-1) # Size of BERT embedding, which is 768 for bert-base
query_layer = nn.Linear(d_model, d_model)
key_layer = nn.Linear(d_model, d_model)
value_layer = nn.Linear(d_model, d_model)
# Apply the linear transformations to get Q, K, and V for all tokens
Q = query_layer(token_embeddings)
K = key_layer(token_embeddings)
V = value_layer(token_embeddings)# Print the results
print("\n Query Vectors for all tokens: \n", Q)
print("\n Key Vectors for all tokens: \n", K)
print("\n Value Vectors for all tokens: \n", V)Output
Query Vectors for all tokens:
tensor([[[ 0.4307, -0.2406, 0.0194, ..., 0.0586, 0.2471, 0.1441],
[ 0.1889, -0.3578, 0.4044, ..., -0.2774, -0.0744, 0.3084],
[-0.1386, 0.0847, 0.3448, ..., 0.3131, -0.1916, 0.2719],
...,
[-0.4465, -0.1400, 0.3623, ..., 0.2517, 0.2243, 0.0794],
[-0.2019, -0.5473, -0.0137, ..., 0.2616, -0.1869, -0.0563],
[ 0.4169, -0.5658, 0.3197, ..., -0.0042, -0.2949, -0.1101]]],
grad_fn=<ViewBackward0>)
Key Vectors for all tokens:
tensor([[[ 0.2980, 0.2993, -0.0512, ..., 0.2682, 0.3186, 0.2025],
[ 0.1551, 0.3881, -0.0096, ..., -0.3588, 0.0626, -0.1446],
[ 0.0576, 0.4083, -0.0733, ..., -0.0838, 0.2047, 0.4594],
...,
[-0.0051, 0.1313, -0.2902, ..., -0.1232, -0.0175, 0.3545],
[ 0.0824, 0.1125, -0.0427, ..., -0.0063, -0.0308, 0.1148],
[ 0.1478, -0.0143, 0.1896, ..., -0.2126, -0.2012, 0.3263]]],
grad_fn=<ViewBackward0>)
Value Vectors for all tokens:
tensor([[[ 0.0580, -0.0339, -0.1754, ..., 0.3090, 0.0182, -0.2084],
[-0.1483, 0.0662, 0.4966, ..., 0.1002, -0.2798, 0.0893],
[ 0.0960, 0.1536, 0.8624, ..., 0.1884, -0.2049, 0.2079],
...,
[-0.5496, -0.6623, 0.4715, ..., -0.2158, -0.5542, -0.2747],
[ 0.3502, -0.1021, 0.4982, ..., 0.5085, -0.0829, 0.0109],
[-0.1685, -0.3038, 0.3571, ..., -0.1949, -0.7392, 0.1081]]],
grad_fn=<ViewBackward0>)Step 2: Compute Attention Scores
The calculation of the attention score between two words starts by taking the dot product of the query of one word and the key of another word. The amount of attention one word should give to another word can be determined by attention score.
# Compute QK^T (transpose of K)
K_T = K.transpose(-1, -2) # Transpose the last two dimensions for correct matmul
# Compute dot product between Q and K^T
attention_scores = torch.matmul(Q, K_T)Step 3: Scale the Attention Scores
The resulting dot product is divided by the square root of the dimension of the key vectors (d_k). By this we can get the scaled value of the dot product. Scaling the dot products avoids sending large values through the softmax layer.
# Scale the attention scores
d_k = Q.size(-1) # This is the hidden dimension (e.g., 768)
scaled_attention_scores = attention_scores / torch.sqrt(torch.tensor(d_k, dtype=torch.float32))d_k represents the dimension of the key/query vector.
Step 4: Apply Softmax to Obtain Attention Weights
Next, the softmax function converts the scaled attention scores into probabilities (also called attention weights). That means all the attention scores will be normalized so adding them together will give a total of 1.
attention_weights = torch.softmax(scaled_attention_scores, dim=-1)print("\n Attention Weights: \n", attention_weights)Output
Attention Weights:
tensor([[[0.0995, 0.0868, 0.0982, 0.0881, 0.0881, 0.0961, 0.0958, 0.0917,
0.0823, 0.0828, 0.0906],
[0.0968, 0.0953, 0.1029, 0.0892, 0.0973, 0.0985, 0.0851, 0.0886,
0.0815, 0.0856, 0.0792],
[0.1005, 0.0936, 0.0963, 0.0909, 0.0909, 0.0940, 0.0847, 0.0835,
0.0796, 0.0900, 0.0958],
[0.0980, 0.0901, 0.1030, 0.0938, 0.0893, 0.0957, 0.0858, 0.0809,
0.0800, 0.0906, 0.0929],
[0.0985, 0.0956, 0.0997, 0.0898, 0.0973, 0.0970, 0.0845, 0.0876,
0.0831, 0.0863, 0.0805],
[0.1007, 0.0926, 0.0991, 0.0909, 0.0869, 0.0935, 0.0884, 0.0809,
0.0818, 0.0930, 0.0922],
[0.0954, 0.0875, 0.0945, 0.0940, 0.0907, 0.0895, 0.0895, 0.0890,
0.0797, 0.0935, 0.0966],
[0.1049, 0.0929, 0.0983, 0.0935, 0.0922, 0.0909, 0.0834, 0.0845,
0.0795, 0.0954, 0.0845],
[0.1018, 0.0889, 0.0967, 0.0940, 0.0902, 0.0916, 0.0885, 0.0873,
0.0782, 0.0946, 0.0883],
[0.1080, 0.0922, 0.0987, 0.0905, 0.0884, 0.0964, 0.0875, 0.0848,
0.0774, 0.0899, 0.0862],
[0.0872, 0.0927, 0.0865, 0.0941, 0.0884, 0.0932, 0.0954, 0.0895,
0.0945, 0.0869, 0.0915]]], grad_fn=<SoftmaxBackward0>)Step 5: Compute Weighted Sum of Values
Weighted sum is obtained by multiplying the attention weights obtained above by values (v). This gives the final attention output for each token.
attention_output = torch.matmul(attention_weights, V)print("\n Attention Output:\n", attention_output)Output
Attention Output:
tensor([[[-0.0130, -0.1833, 0.1295, ..., 0.2356, -0.3097, -0.0799],
[-0.0135, -0.1813, 0.1297, ..., 0.2444, -0.3079, -0.0720],
[-0.0223, -0.1883, 0.1333, ..., 0.2325, -0.3037, -0.0828],
...,
[-0.0153, -0.1819, 0.1301, ..., 0.2390, -0.3037, -0.0786],
[-0.0177, -0.1767, 0.1346, ..., 0.2430, -0.3015, -0.0754],
[-0.0139, -0.1952, 0.1204, ..., 0.2302, -0.3151, -0.0861]]],
grad_fn=<UnsafeViewBackward0>)Scaled Dot Product Attention Implementation (PyTorch)
In this scaled dot product attention I used BERT for tokenization and input token embedding. BERT uses 768 dimensional vectors for input embeddings. In the Multi head attention implementation section, you will see that I did not use pre trained embeddings instead I trained them from scratch.
import torch
import torch.nn as nn
from transformers import BertTokenizer, BertModel
# Load pre-trained BERT model and tokenizer
tokenizer = BertTokenizer.from_pretrained('bert-base-uncased')
model = BertModel.from_pretrained('bert-base-uncased')
model.eval()
# Tokenize the input sentence
sentence = "The cat chased the mouse because it was hungry"
inputs = tokenizer(sentence, return_tensors='pt')
# Get BERT embeddings for all tokens in the sentence
with torch.no_grad():
outputs = model(**inputs)
# Extract token embeddings from BERT's last hidden state
token_embeddings = outputs.last_hidden_state
# Define Linear Layers for Query, Key, and Value projections
d_model = token_embeddings.size(-1) # Size of BERT embedding, which is 768 for bert-base
query_layer = nn.Linear(d_model, d_model)
key_layer = nn.Linear(d_model, d_model)
value_layer = nn.Linear(d_model, d_model)
# Apply the linear transformations to get Q, K, and V for all tokens
Q = query_layer(token_embeddings)
K = key_layer(token_embeddings)
V = value_layer(token_embeddings)
# Scaled Dot-Product Attention
# Compute QK^T (transpose of K)
K_T = K.transpose(-1, -2) # Transpose the last two dimensions for correct matmul
# Compute dot product between Q and K^T
attention_scores = torch.matmul(Q, K_T)
# Scale the attention scores
d_k = Q.size(-1) # This is the hidden dimension (e.g., 768)
scaled_attention_scores = attention_scores / torch.sqrt(torch.tensor(d_k, dtype=torch.float32))
# Apply softmax to get attention weights
attention_weights = torch.softmax(scaled_attention_scores, dim=-1)
# Use the attention weights to compute weighted sum of Value (V) vectors
attention_output = torch.matmul(attention_weights, V)Multi Head Attention
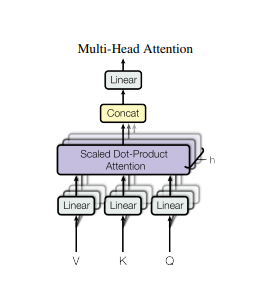
It is more effective to project keys, values and queries with different learned weight metrics multiple times rather than performing the attention function only once for keys, values and queries with d_model (512) dimension as done in the previous step.
Projection of Queries, Keys, and Values
Each token embedding is projected into query, key, and value vectors using learned weight metrices. Then they are divided into multiple parts or subspaces (called heads).
For example, If each token embedding has dimension size of 512 (d_model) and 8 heads (h) to be used, each head is given a portion of query, key, and value vectors of dimension size of d_k = 64 (512/8).
assert d_model % num_heads == 0, "d_model must be divisible by num_heads"
# Dimensionality per head
d_k = d_model // num_heads
# Linear layers to project the input queries, keys, and values
W_q = nn.Linear(d_model, d_model)
W_k = nn.Linear(d_model, d_model)
W_v = nn.Linear(d_model, d_model)
# Apply linear transformations to the input queries, keys, and values
Q = W_q(Q)
K = W_k(K)
V = W_v(V)
batch_size = Q.shape[0]
# Reshape and transpose the queries, keys, and values for multi-head attention
# Shape of Q, K, and V for each head : (batch_size, num_heads, seq_len, d_k)
Q = Q.view(batch_size, -1, num_heads, d_k).transpose(1, 2)
K = K.view(batch_size, -1, num_heads, d_k).transpose(1, 2)
V = V.view(batch_size, -1, num_heads, d_k).transpose(1, 2)Scaled Dot Product Attention
Next it calculates the scaled dot product attention for each head separately. Thus each of them will calculate different attention. Each will focus on different relationships between tokens.
For example,
- Head 1 may focus attention on distantly related tokens in a long sentence.
- Head 2 may focus on the syntax of the sentence. It may be focused on the subject-verb-object relationship to capture grammar.
- Head 3 may understands the relationship between adjacent tokens by attending to them.
Thus each of the 8 heads will focus on different aspects. We use 8 for no of heads based on the original paper. you can experiment with different values and choose the one perform best.
For instance LLaMA 3 uses 32 heads and incorporates some advanced concepts like key value caching(kv cache), rotary positional encoding and more, Which we will try to explore in upcoming articles.
You can also check out the source code of llma3 from github. Navigate to llma > model.py inside the given repo in order to read the multi head attention mechanism implementation.
dropout = nn.Dropout(dropout)
attn_scores = torch.matmul(Q, K.transpose(-2, -1)) / math.sqrt(self.d_k)
# Apply mask if provided (mask out positions with large negative value)
if mask is not None:
attn_scores = attn_scores.masked_fill(mask == 0, -1e9)
attn_probs = torch.softmax(attn_scores, dim=-1)
if dropout is not None:
attn_probs = dropout(attn_probs)
attn_output = torch.matmul(attn_probs, V)Multi-Head Attention
Once the attention output is computed for each individual head, they are combined together. Each attention result consists of 64 dimensions. After concatenating all the 8 heads, the dimension of the result will be 512. This is the same size as the original input embedding.
attn_output = attn_output.transpose(1, 2).contiguous().view(attn_output.shape[0], -1, num_heads * d_k)Finally, the concatenated output is passed to a linear layer. Here the information in all the heads will be mixed together. In this linear layer the concatenated attention output is multiplied by the trained weight matrix W_0.
output = W_o(attn_output)Multi Head Attention Implementation (PyTorch)
import torch
import torch.nn as nn
import math
class MultiHeadAttention(nn.Module):
def __init__(self, d_model: int, num_heads: int, dropout: float):
"""
Initializes the Multi-Head Attention module.
Args:
- d_model: Dimensionality of the input embeddings (e.g., 512).
- num_heads: Number of attention heads (e.g., 8).
- dropout: Dropout probability applied to the attention probabilities.
"""
super().__init__()
self.d_model = d_model
self.num_heads = num_heads
assert d_model % num_heads == 0, "d_model must be divisible by num_heads"
# Dimensionality per head
self.d_k = d_model // num_heads
# Linear layers to project the input queries, keys, and values
self.W_q = nn.Linear(d_model, d_model, bias=False)
self.W_k = nn.Linear(d_model, d_model, bias=False)
self.W_v = nn.Linear(d_model, d_model, bias=False)
# Linear layer for the final output projection
self.W_o = nn.Linear(d_model, d_model, bias=False)
# Dropout layer applied after softmax
self.dropout = nn.Dropout(dropout)
def scaled_dot_product_attention(self, Q: torch.Tensor, K: torch.Tensor, V: torch.Tensor, mask: torch.Tensor = None) -> torch.Tensor:
"""
Compute scaled dot-product attention.
Args:
- Q: Queries tensor of shape (batch_size, num_heads, seq_len, d_k).
- K: Keys tensor of shape (batch_size, num_heads, seq_len, d_k).
- V: Values tensor of shape (batch_size, num_heads, seq_len, d_k).
- mask: Mask tensor to avoid attending to certain positions.
Returns:
- attn_output: Output after applying attention of shape (batch_size, num_heads, seq_len, d_k).
"""
attn_scores = torch.matmul(Q, K.transpose(-2, -1)) / math.sqrt(self.d_k)
# Apply mask if provided (mask out positions with large negative value)
if mask is not None:
attn_scores = attn_scores.masked_fill(mask == 0, -1e9)
attn_probs = torch.softmax(attn_scores, dim=-1)
if self.dropout is not None:
attn_probs = self.dropout(attn_probs)
attn_output = torch.matmul(attn_probs, V)
return attn_output
def forward(self, Q: torch.Tensor, K: torch.Tensor, V: torch.Tensor, mask: torch.Tensor = None) -> torch.Tensor:
# Apply linear transformations to the input queries, keys, and values
Q = self.W_q(Q)
K = self.W_k(K)
V = self.W_v(V)
batch_size = Q.shape[0]
# Reshape and transpose the queries, keys, and values for multi-head attention
# Shape of Q, K, and V for each head : (batch_size, num_heads, seq_len, d_k)
Q = Q.view(batch_size, -1, self.num_heads, self.d_k).transpose(1, 2)
K = K.view(batch_size, -1, self.num_heads, self.d_k).transpose(1, 2)
V = V.view(batch_size, -1, self.num_heads, self.d_k).transpose(1, 2)
# Compute the scaled dot-product attention
attn_output = self.scaled_dot_product_attention(Q, K, V, mask)
# Combine heads and apply the final linear transformation
attn_output = attn_output.transpose(1, 2).contiguous().view(attn_output.shape[0], -1, self.num_heads * self.d_k)
output = self.W_o(attn_output)
return output# Example usage
if __name__ == "__main__":
batch_size = 64 # Number of samples in a batch
seq_len = 10 # Length of input sequence
d_model = 512 # Dimensionality of the input embeddings
num_heads = 8 # Number of attention heads
# Create a random input tensor (Q, K, V)
Q = torch.randn(batch_size, seq_len, d_model)
K = torch.randn(batch_size, seq_len, d_model)
V = torch.randn(batch_size, seq_len, d_model)
# Optional mask (for example, to mask out padding tokens)
mask = None
dropout = 0.1
# Initialize the multi-head attention layer
mha = MultiHeadAttention(d_model=d_model, num_heads=num_heads, dropout=dropout)
# Forward pass through the multi-head attention layer
output = mha(Q, K, V, mask)
# Output shape: (batch_size, seq_len, d_model)
print(output.shape) # Should print: torch.Size([64, 10, 512])In the code:
I used a dropout layer, which is used to prevent overfitting. It works by randomly selecting a subset of neurons and deactivating their outputs during each forward pass. But in the newer Transformer architectures, dropout is not used as much. There are few factors contribute to this.
- In the Transformer architecture diagram you can see LayerNorm, which helps stabilize the training and reduces the need of additional regularization methods such as dropout.
- Many of the LLM models are trained on large amount of data which naturally provide enough regularization and reducing the risk of overfitting.
- There is another regularization method called Weight Decay is used during training, which apply small modifications to the weights to reduce overfitting, making dropout less needed.
Some parts of the models still using dropout especially during fine tuning and some models trained on or handling smaller dataset still using dropout.
If you do not want to use dropout layer inside your MultiHeadAttention you can choose to remove the dropout code entirely or specify dropout = 0.0 to not to apply dropout (the layer will still be created) but the layer will not make much impact to the overall training.
If you do not want the dropout layer to be created unless a dropout value is provided, then you can use the following code instead.
self.dropout = nn.Dropout(dropout) if dropout is not None else NoneAlso instead of setting dropout = 0.0 or dropout = 0.1 set dropout = None.

