What is a Transformer?
Transformer is a deep learning model introduced in the 2017 research paper ‘Attention is All You Need’ by Vaswani et al. Later, many state-of-the-art natural language models, such as BERT, GPT, and T5, were developed based on the Transformer architecture.
Why Transformers Over RNNs?
Sequential Processing
Unlike earlier models such as RNN and LSTM, Transformers completely relies on the attention mechanism. We will discuss the attention mechanism later.
A recurrent neural network (RNN) can process only one step at a time. This means only one word can be handled at a time in a sentence, so in order to understand the context of the current processing word all the previous words must be remembered. Therefore, RNN network training is very slow especially if long sequences are given.
But transformers can process multiple words in a sentence at the same time without needing to handle each word individually. This allows transformers to be trained much faster compared to training RNN. Imagine you are reading a book, RNN processes each word or sentence in it while the transformer scans the entire page once and identifies the relationships between the words or sentences in it.
Vanishing Gradient Problem
When doing RNN training, we will use the method called backpropagation, which will calculate the gradients and propagate backward through the network.
When dealing with long sequences in RNN training, the gradients calculated in backpropagation will be very small. The small gradients calculated become smaller(become vanish) as the backpropagation is repeated many times, which makes it even more difficult for the network to learn and remember the earlier information in the sequence.
Calculating gradients and things like math behind Vanishing Gradients are not explained in depth here, knowledge about them can be obtained in deep learning.
The Transformer Architecture: An Overview
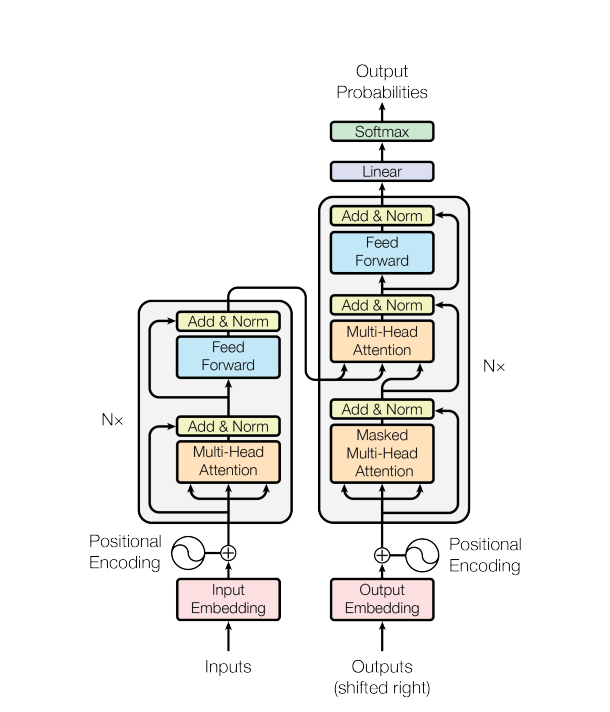
Transformer follows encoder-decoder structure. Both encoder and decoder have multiple layers within them (usually 6). Each of those layers has subcomponents like Multi-head attention and feed forward network.
- Encoder (Left): Reads input data and converts into a format so that its meaning can be captured.
- Decoder (Right): The job of the decoder is to convert the information from the encoder into the required output.
Encoder
An encoder reads the input data (like a sentence) and converts it into a format that allowing it to capture the relationships between the words.
Let’s say, A person reading a sentence and understanding the relationship between words in it (Encoder). Then they can be explained to someone else (Decoder).
The Encoder is made up of many identical layers (usually 6). Each of these layers has 2 main components.
- Multi-head Self-Attention Mechanism
- Feed-Forward Network (FFN)
In addition to these, there are other key components that help these layers work better.
- Positional Encoding
- Residual Connections and Layer Normalization
Input Embedding
In input embedding, each word in the input sequence or sentence is mapped to a high-dimensional vector of numbers. We call these as ’embeddings’ and they contain the semantic information of those words.
Why Do We Need Embeddings?
Machine learning models do not deal with raw text directly, so words are converted into numerical representations. However, If each word is assigned a unique number (e.g., ‘apple’ = 1, ‘orange’ = 2) it can’t capture a lot of information such as their meaning, similarity. For example:
- The words “banana” and “fruit” are related to each other, but a simple numbering system like the one above cannot reflect that.
words are converted into embeddings to add more meaningful information. In a large multi-dimensional space, words with similar meaning are located near while words with different meaning are located far away. For example:
- “book” is close to “read” and “study”.
- “car” is far from “book” but near to “drive”.
How Embeddings Work
Let’s say, we have a vocabulary (a list of all possible words) of v (e.g., 50257). We should represent each word as a vector of size d_model (e.g., 512).
While working on projects, We give values like 512 or 1024 for d_model depending on the complexity of the model. Some models have a value of 768. You can experiment with different values to select the one that performs well.
For example, if the vocabulary size is 50257 and d_model size is 512 for the embedding layer, training will generate 50257 vector embeddings as shown below. Each vector embedding contains 512 dimensions.
tensor([
[-0.0911, 0.4307, -0.1428, ..., 0.5158, -1.3606, -0.1638],
[-0.8179, 0.4711, -2.0562, ..., 0.4006, 0.9923, -0.4150],
[-2.4794, 0.6483, 1.3902, ..., 1.2597, 1.3406, 0.5898],
...,
[-0.0336, -0.0860, -0.0774, ..., 1.1049, 1.0227, -1.6652],
[ 0.5579, 0.8344, 1.3910, ..., 0.5587, -1.2766, 0.4206],
[-0.0701, -1.2426, -0.8822, ..., -1.1367, 1.6942, 0.1455]
])Here each embedding in each row indicates to a unique word, with a specific token ID is given to them. Here the token ID starts from 0 and goes up to 50256.
If a word (token) is passed to the model, then the token will be converted to the corresponding token ID and search for the token embedding inside the embedding layer of size (v x d_model) (e.g., 50257 * 512).
Key Steps in Input Embedding
Tokenize the Sentence
First, the input sentence is divided into tokens. Generally those tokens are words or subwords depending on the tokenizer used.
- sentence = “The cat chased the mouse because it was hungry”
- Tokens: [‘the’, ‘cat’, ‘chased’, ‘the’, ‘mouse’, ‘because’, ‘it’, ‘was’, ‘hungry’]
Byte-Pair Encoding(BPE) is the most common subword tokenization method used in Transformers. It is used to handle rare or out-of-vocabulary words. It breaks them into small pieces (subwords).
- The word “unhappiness” can be broken down as [“un”, “happiness”].
- The word “happiness” can also be broken down into smaller pieces [“hap”, “pi”, “ness”] if needed.
The model learns how to represent full words (e.g., “happiness” ) by combining each broken subword (e.g., “hap”, “pi”, “ness”) with its own embedding.
Embedding Lookup
For each token segmented above, the corresponding embedding is searched in the embedding matrix created earlier in the embedding layer. Embedding is obtained by searching the token ID of a particular word in the embedding matrix.
Input Embedding Implementation (PyTorch)
import torch
import math
import torch.nn as nn
class InputEmbeddings(nn.Module):
def __init__(self, vocab_size: int, d_model: int):
super().__init__()
self.d_model = d_model
self.vocab_size = vocab_size
self.embedding = nn.Embedding(vocab_size, d_model)
def forward(self, x):
# Multiply by sqrt(d_model) to scale the embeddings according to the paper
return self.embedding(x) * math.sqrt(self.d_model)# Example usage
from transformers import GPT2Tokenizer
# Use GPT-2 tokenizer for tokenizing raw text
tokenizer = GPT2Tokenizer.from_pretrained('gpt2')
# Add a new pad token if it doesn't exist already
if tokenizer.pad_token is None:
tokenizer.add_special_tokens({'pad_token': '[PAD]'})
# Example raw text input
sentence = "I am learning how transformers work."
# Tokenize the input text: Convert to token indices
tokens = tokenizer(sentence, padding=True, truncation=True, max_length=50, return_tensors='pt')
# Get the token indices
input_ids = tokens['input_ids']
print('input_ids: ', input_ids)
# Initialize input embedding layer
vocab_size = len(tokenizer)
d_model = 512 # Embedding size according to the Transformer paper
input_embedding_layer = InputEmbeddings(vocab_size=vocab_size, d_model=d_model)
# Forward pass: obtain the embeddings
embeddings = input_embedding_layer(input_ids)
# Output shape: (batch_size, sequence_length, d_model)
print(f"Embeddings shape: {embeddings.shape}")
print(f"Embeddings: \n {embeddings}")Output
input_ids: tensor([[ 40, 716, 4673, 703, 6121, 364, 670, 13]])
Embeddings shape: torch.Size([1, 8, 512])
Embeddings:
tensor([[[-34.0023, -4.4200, 8.5418, ..., -35.5519, 0.3757, -32.1044],
[ 28.9763, -28.8719, 5.5829, ..., 5.8646, -13.2516, -27.5301],
[ 18.8462, 3.8231, 6.6916, ..., 53.6452, -23.7118, -5.8930],
...,
[-47.3805, 25.9221, -43.8729, ..., 25.6585, -25.2883, 33.3656],
[-15.6482, 2.4699, -21.0274, ..., 34.8424, 31.9267, -43.2403],
[-19.6558, 7.9178, 19.7607, ..., 4.6041, 32.0807, 19.4441]]],
grad_fn=<MulBackward0>)In the above code:
GPT2 tokenizer has been used for tokenization in the above code. The reason is that it is already trained on a large amount of text using byte-pair encoding (resulting a vocabulary of 50257 tokens) Due to that most of the words can be tokenized.
If you want to gain in-depth knowledge about tokenizers and learn many different ways to implement tokenizers for all the models, read the Tokenizer library from hugging face.
The shape: torch.Size([1, 8, 512]) represents the following ([batch_size, sequence_length, hidden_size]). It corresponds to them in this order: ([No of sentences passed in input, Token count of the sentence, Vector dimension of each token]).
Multiple sentences can be input instead of one sentence. For that, the above code should be modified as given below.
sentences = [
"I am learning how transformers work",
"The cat chased the mouse because it was hungry"
]
tokens = tokenizer(sentences, padding=True, truncation=True, max_length=50, return_tensors='pt')Output
Embeddings shape: torch.Size([2, 9, 512])
input_ids: tensor([[ 40, 716, 4673, 703, 6121, 364, 670, 50257, 50257],
[ 464, 3797, 26172, 262, 10211, 780, 340, 373, 14720]])torch.Size([2, 9, 512]): Batch size became 2 because 2 sentences are passed in the input, Second sentence is the longest sentence with 9 tokens, so the sequence length is 9 in Embedding shape.
padding=True: This is applied only when the sentences have different lengths. 1st sentence is split into 7 tokens. Two padding tokens [PAD] (Token ID: 50257) have been added at the last to equalize it with token count 9 of the longest sentence. The default is to add padding tokens at the end of the sentence tokens, but this can be customized.
truncation=True, max_length=50: If the token length of the input sentence exceeds 50, additional tokens will be cut off (truncate).
If padding=’max_length’ is given along with max_length=50 then, This ensures all the token sequences are padded to exactly 50 tokens. Padding tokens will be added in additional spaces to make the token length of each sentence to exactly 50. Like shown below:
Embeddings shape: torch.Size([2, 50, 512])
input_ids: tensor([[ 40, 716, 4673, 703, 6121, 364, 670, 50257, 50257, 50257,
50257, 50257, 50257, 50257, 50257, 50257, 50257, 50257, 50257, 50257,
50257, 50257, 50257, 50257, 50257, 50257, 50257, 50257, 50257, 50257,
50257, 50257, 50257, 50257, 50257, 50257, 50257, 50257, 50257, 50257,
50257, 50257, 50257, 50257, 50257, 50257, 50257, 50257, 50257, 50257],
[ 464, 3797, 26172, 262, 10211, 780, 340, 373, 14720, 50257,
50257, 50257, 50257, 50257, 50257, 50257, 50257, 50257, 50257, 50257,
50257, 50257, 50257, 50257, 50257, 50257, 50257, 50257, 50257, 50257,
50257, 50257, 50257, 50257, 50257, 50257, 50257, 50257, 50257, 50257,
50257, 50257, 50257, 50257, 50257, 50257, 50257, 50257, 50257, 50257]])Positional Encoding
In natural language order of words is important. For example, the meaning of the sentence “The cat sat on the mat” and “The mat sat on the cat” are different. We humans can understand the change of meaning as the order of words changes, but Transformer cannot inherently understand it.
RNN processes each word in a sequence or sentence one by one, so they naturally know the order of words, but Transformers process many words at the same time (in parallel), so there is no information about word order.
Transformers use positional encoding to address this problem. The positional encoding generated here is added to the embedding of each word.
How Positional Encoding Works
A unique vector (Positional encoding) for each word in the input sequence or sentence is calculated using sinusoidal equation. The positional encodings have the same length of d_model as the word embeddings, so that both of them can be summed.
Input embeddings are learned during training while positional encodings are calculated using mathematical formulas based on sine and cosine functions. So, positional encoding vectors are fixed for each position in the sequence.
The math behind positional encoding can be a little confusing, but I have explained it below in a way that makes it easy to understand.
Two different equations are used for even and odd dimensions of the word embeddings while calculating positional encodings.
For even dimensions
For odd dimensions
I will use the sentence “He is learning” to demonstrate the math behind positional encoding. Here, to show the steps of the math calculations easily I assumed that the embedding dimension (d_model) of each word is 4, instead of 512.
Positional encoding will be calculated for each token in the sentence. I am assuming that the first word “He” in position 0 (pos = 0) has been assigned a 4 dimensional word embedding of [0.5, -0.3, 1.2, 0.7] in input embedding step.
[0.5, -0.3, 1.2, 0.7] There are 4 values in the above word embedding and its indexes are 0, 1, 2, 3 in which 0, 2 are even dimensions and 1, 3 are odd dimensions. We use different equations for even and odd dimensions to calculate positional encoding.
In the sinusoidal equations “i” represents the index of the values in the word embedding. This part can be a bit confusing so pay close attention.
In sinusoidal equations the values of “i” are calculated separately for even and odd dimensions. If even dimensions (0, 2) are considered as separate vector ([0, 2]) then their indices will be 0, 1 ( i ).
Similarly, for odd dimensions (1, 3) their indices will be 0 and 1 (i).
Let’s start with the embedding of the word “He” at position 0 (pos = 0): [0.5, -0.3, 1.2, 0.7]
- Dimension 0 (0.5): 0 is an even number so we use the equation for even dimensions. Since 0 is at index 0 in the vector we assumed with only even dimensions, It assigns i = 0 and 2i = 0 .
- Dimension 1 (-0.3): 1 is an odd number so we use the equation for odd numbers. Since 1 is in index 0 of odd dimensions so i = 0 here too. So, 2i = 0 and 2i + 1 = 1 .
- Dimension 2 (1.2): 2 is an even number so we use equation for even number. Here 2 is at index 1 of even dimensions so here i = 1. According to it 2i = 2 .
- Dimension 3 (0.7): 3 is an odd number so we use the equation for odd numbers. Here 3 is at index 1 of odd dimensions so i = 1. Hence, 2i = 2 and 2i + 1 = 3.
Finally, the positional encoding for the word “He” at position 0 is:
PE(0) = [0,1,0,1]After calculating the positional encoding, those values are summed with the word embedding.
After the positional encoding for “He” is calculated in position 0, We move on to the next words. Next, positional encoding is calculated for “is” at position 1 (pos = 1) and “learning” at position 2 (pos = 2) and then added to their respective word embeddings.
Positional Encoding Implementation (PyTorch)
import torch
import math
import torch.nn as nn
class PositionalEncoding(nn.Module):
def __init__(self, d_model, max_len=5000):
super(PositionalEncoding, self).__init__()
self.d_model = d_model # Store the embedding dimension
self.max_len = max_len
# Create a matrix of max_len by d_model to store positional encodings
pe = torch.zeros(max_len, d_model)
position = torch.arange(0, max_len, dtype=torch.float).unsqueeze(1)
# Compute the division term for sine and cosine
div_term = torch.exp(torch.arange(0, d_model, 2).float() * (-math.log(10000.0) / d_model))
# Apply sine to even dimensions (0, 2, 4, ...)
pe[:, 0::2] = torch.sin(position * div_term)
# Apply cosine to odd dimensions (1, 3, 5, ...)
pe[:, 1::2] = torch.cos(position * div_term)
pe = pe.unsqueeze(0) # Shape it to (1, max_len, d_model)
# Register pe as a buffer to avoid updating it during training
self.register_buffer('pe', pe)
def forward(self, x):
# Add positional encoding to input embeddings
x = x + (self.pe[:, :x.shape[1], :]).requires_grad_(False)
return x# Example usage
from transformers import GPT2Tokenizer
tokenizer = GPT2Tokenizer.from_pretrained('gpt2')
if tokenizer.pad_token is None:
tokenizer.add_special_tokens({'pad_token': '[PAD]'})
sentence = "I am learning how transformers work."
tokens = tokenizer(sentence, padding=True, truncation=True, max_length=50, return_tensors='pt')
input_ids = tokens['input_ids']
vocab_size = len(tokenizer)
d_model = 512
input_embedding_layer = InputEmbeddings(vocab_size=vocab_size, d_model=d_model)
embeddings = input_embedding_layer(input_ids)
# Initialize positional encoding layer
pos_encoding_layer = PositionalEncoding(d_model=d_model, max_len=embeddings.shape[1])
# Apply positional encoding to embeddings
pos_encoded_embeddings = pos_encoding_layer(embeddings)
print(f"Shape of embeddings alone: {embeddings.shape}")
print(f"Embeddings before positional encoding added: \n {embeddings}")
pe = pos_encoding_layer.pe
print(f"Positional encoding shape: {pe.shape}")
print(f"Positional encodings: \n {pe}")
print(f"After positional encoding added: \n {pos_encoded_embeddings}")Output
Shape of embeddings alone: torch.Size([1, 8, 512])
Embeddings before positional encoding added:
tensor([[[-34.0023, -4.4200, 8.5418, ..., -35.5519, 0.3757, -32.1044],
[ 28.9763, -28.8719, 5.5829, ..., 5.8646, -13.2516, -27.5301],
[ 18.8462, 3.8231, 6.6916, ..., 53.6452, -23.7118, -5.8930],
...,
[-47.3805, 25.9221, -43.8729, ..., 25.6585, -25.2883, 33.3656],
[-15.6482, 2.4699, -21.0274, ..., 34.8424, 31.9267, -43.2403],
[-19.6558, 7.9178, 19.7607, ..., 4.6041, 32.0807, 19.4441]]],
grad_fn=<MulBackward0>)
Positional encoding shape: torch.Size([1, 8, 512])
Positional encodings:
tensor([[[ 0.0000e+00, 1.0000e+00, 0.0000e+00, ..., 1.0000e+00,
0.0000e+00, 1.0000e+00],
[ 8.4147e-01, 5.4030e-01, 8.2186e-01, ..., 1.0000e+00,
1.0366e-04, 1.0000e+00],
[ 9.0930e-01, -4.1615e-01, 9.3641e-01, ..., 1.0000e+00,
2.0733e-04, 1.0000e+00],
...,
[-9.5892e-01, 2.8366e-01, -9.9385e-01, ..., 1.0000e+00,
5.1832e-04, 1.0000e+00],
[-2.7942e-01, 9.6017e-01, -4.7522e-01, ..., 1.0000e+00,
6.2198e-04, 1.0000e+00],
[ 6.5699e-01, 7.5390e-01, 4.5239e-01, ..., 1.0000e+00,
7.2564e-04, 1.0000e+00]]])
After positional encoding added:
tensor([[[-34.0023, -3.4200, 8.5418, ..., -34.5519, 0.3757, -31.1044],
[ 29.8178, -28.3316, 6.4047, ..., 6.8646, -13.2515, -26.5301],
[ 19.7555, 3.4069, 7.6280, ..., 54.6452, -23.7116, -4.8930],
...,
[-48.3394, 26.2058, -44.8668, ..., 26.6585, -25.2878, 34.3656],
[-15.9276, 3.4300, -21.5027, ..., 35.8424, 31.9273, -42.2403],
[-18.9988, 8.6717, 20.2131, ..., 5.6041, 32.0814, 20.4441]]],
grad_fn=<AddBackward0>)
